Giải bài 6 trang 79 vở thực hành Toán 7 tập 2
Cho tam giác ABC vuông tại A có góc B bằng ({60^o}). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (left( {M in BC} right)). a) Chứng minh (Delta ABE = Delta MBE). b) Chứng minh (MB = MC). c) Gọi I là giao điểm của BA và ME. Chứng minh (IE > EM).
Đề bài
Cho tam giác ABC vuông tại A có góc B bằng \({60^o}\). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC \(\left( {M \in BC} \right)\).
a) Chứng minh \(\Delta ABE = \Delta MBE\).
b) Chứng minh \(MB = MC\).
c) Gọi I là giao điểm của BA và ME. Chứng minh \(IE > EM\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(\widehat {BAE} = \widehat {BME} = {90^o},\widehat {ABE} = \widehat {EBM},BE\;chung\) nên \(\Delta ABE = \Delta MBE\).
b) Chứng minh \(\widehat {EBC} = \widehat C = {30^o}\) nên tam giác BEC cân tại E, suy ra EM là đường cao đồng thời là đường trung tuyến, suy ra \(MB = MC\).
c) + Chứng minh tam giác AEI vuông tại A nên \(IE > AE\)
+ Vì \(\Delta ABE = \Delta MBE\) nên \(AE = EM\). Do đó, \(IE > EM\).
Lời giải chi tiết
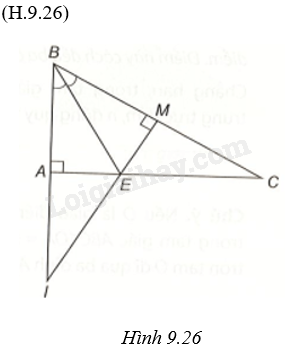
a) Xét hai tam giác vuông ABE và MBE, ta có:
\(\widehat {BAE} = \widehat {BME} = {90^o},\widehat {ABE} = \widehat {EBM},BE\;chung\)
Do đó, \(\Delta ABE = \Delta MBE\) (cạnh huyền – góc nhọn)
b) Trong tam giác vuông ABC, ta có \(\widehat B = {60^o}\) nên \(\widehat C = {30^o}\).
Vì BE là phân giác của \(\widehat {ABC}\) nên \(\widehat {ABE} = \widehat {EBM} = \frac{{\widehat {ABC}}}{2} = {30^o}\)
Vậy tam giác BEC có \(\widehat {EBC} = \widehat C = {30^o}\) nên tam giác BEC cân tại E.
Tam giác BEC cân tại E và có EM là đường cao đồng thời là đường trung tuyến, suy ra \(MB = MC\).
c) Ta có góc BAE kề bù với góc IAE nên \(\widehat {IAE} = {90^o}\).
Trong tam giác vuông AEI có cạnh IE là cạnh huyền nên \(IE > AE\) (1)
Theo câu a) \(\Delta ABE = \Delta MBE\) nên \(AE = EM\) (2)
Từ (1) và (2) suy ra \(IE > EM\).


