Danh Mục
-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Giải bài 19 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình lập phương (ABCD cdot A'B'C'D') có cạnh bằng (a). Góc giữa hai đường thẳng (AC) và (BC') bằng
Đề bài
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có cạnh bằng \(a\). Góc giữa hai đường thẳng \(AC\) và \(BC'\) bằng
A. \({90^ \circ }\).
B. \({30^ \circ }\).
C. \({60^ \circ }\).
D. \({45^ \circ }\).
Phương pháp giải - Xem chi tiết
Phương pháp
Ta có \(AC//A'C' \Rightarrow \left( {AC,BC'} \right) = \left( {A'C',BC'} \right)\)
Nhận dạng tam giác \(BA'C'\) đều \( \Rightarrow \left( {A'C',BC'} \right) = {60^ \circ }\)
Quảng cáo
Lời giải chi tiết
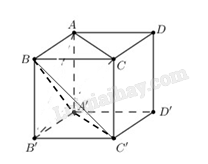
Ta có \(AC//A'C' \Rightarrow \left( {AC,BC'} \right) = \left( {A'C',BC'} \right)\)
Xét tam giác \(BA'C'\) có ba cạnh là ba đường chéo của 3 hình vuông bằng nhau nên tam giác \(BA'C'\) đều. Vậy \(\left( {AC,BC'} \right) = \left( {A'C',BC'} \right) = {60^ \circ }\)
Chọn C