Danh Mục

Giải bài 1 (9.27) trang 82 vở thực hành Toán 7 tập 2


Cho tam giác ABC có (widehat A = {100^o}) và trực tâm H. Tính góc BHC.

Đề bài

Cho tam giác ABC có \(\widehat A = {100^o}\) và trực tâm H. Tính góc BHC.

Phương pháp giải - Xem chi tiết

+ Gọi ba đường cao AI, BJ, CK đồng quy tại H của tam giác ABC.

+ Chỉ ra: \(\widehat {{H_1}} + \widehat {{A_1}} = {90^o}\), $\widehat{{{H}_{2}}}+\widehat{{{A}_{2}}}={{90}^{o}}$ suy ra \(\widehat {BHC} + \widehat {JAK} = {180^o}\), từ đó tính được góc BHC.

Lời giải chi tiết

(H.9.33)

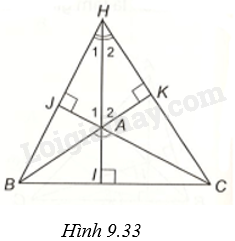
Ta kí hiệu các đường cao AI, BJ, CK đồng quy tại H và các góc như hình vẽ.

Trong tam giác vuông JHA có \(\widehat {{H_1}} + \widehat {{A_1}} = {90^o}\).

Trong tam giác vuông KHA có \(\widehat {{H_2}} + \widehat {{A_2}} = {90^o}\).

Suy ra \(\widehat {{H_1}} + \widehat {{A_1}} + \widehat {{H_2}} + \widehat {{A_2}} = {180^o}\), hay \(\widehat {{H_1}} + \widehat {{H_2}} + \widehat {{A_1}} + \widehat {{A_2}} = {180^o}\), tức là \(\widehat {BHC} + \widehat {JAK} = {180^o}\).

Ta lại có \(\widehat {JAK} = \widehat {BAC} = {100^o}\), suy ra \(\widehat {BHC} = {180^o} - {100^o} = {80^o}\).


© 2025 Luyện Thi 24/7. All Rights Reserved