Bài 9. Đồ thị quãng đường - thời gian trang 55, 56, 57, 58 Khoa học tự nhiên 7 Chân trời sáng tạo
Để mô tả chuyển động của một vật, như chiếc ca nô ở hình bên, người ta có thể sử dụng những cách nào. Dựa vào Bảng 9.1, hãy thực hiện các yêu cầu sau. Nêu nhận xét về đường nối các điểm O, A, B, C, D trên Hình 9.2 (thẳng hay cong, nghiêng hay nằm ngang).
Câu hỏi tr 55 MĐ
|
Để mô tả chuyển động của một vật, như chiếc ca nô ở hình bên, người ta có thể sử dụng những cách nào?
|
Phương pháp giải:
Quan sát hình ảnh và vận dụng kiến thức đã học
Lời giải chi tiết:
Để mô tả chuyển động của một vật, người ta có thể biểu diễn chuyển động thông qua đồ thị quãng đường – thời gian.
Câu hỏi tr 55 CH 1
|
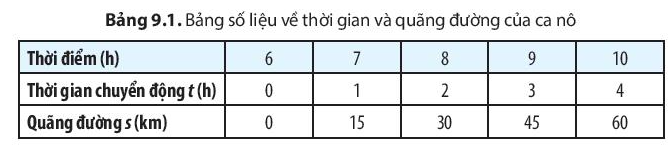
1. Dựa vào Bảng 9.1, hãy thực hiện các yêu cầu sau:
a) Xác định thời gian để ca nô đi được quãng đường 60 km. b) Tính tốc độ của ca nô trên quãng đường 60 km. c) Dự đoán vào lúc 9 h, ca nô sẽ đi đến vị trí cách bến bao nhiêu km. Cho biết tốc độ của ca nô không đổi. |
Phương pháp giải:
Quan sát và phân tích bảng số liệu
Biểu thức tính tốc độ: \(v = \frac{s}{t}\)
Lời giải chi tiết:
a) Dựa vào bảng 9.1, ta có thời gian để ca nô đi được quãng đường 60 km là 4 h
b) Tốc độ của ca nô trên quãng đường 60 km là:
\(v = \frac{s}{t} = \frac{{60}}{4} = 15(km/h)\)
c) Ca nô xuất phát lúc 6 h, kết thúc lúc 9 h
=> Thời gian chuyển động của ca nô là 9 – 6 = 3 h
Quãng đường ca nô đi được là: s = v.t = 15.3 = 45 km
Câu hỏi tr 56 CH 2
|
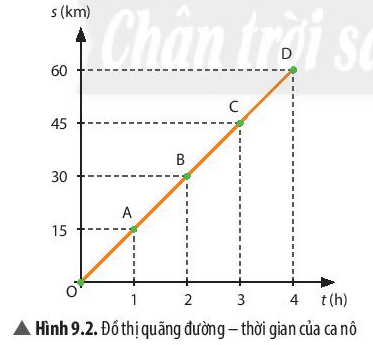
2. Nêu nhận xét về đường nối các điểm O, A, B, C, D trên Hình 9.2 (thẳng hay cong, nghiêng hay nằm ngang).
|
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Từ hình 9.2, ta thấy đường nối các điểm O, A, B, C, D là đường thẳng, nghiêng so với phương ngang.
Câu hỏi tr 56 LT
| Dựa vào bảng ghi số liệu dưới đây về quãng đường và thời gian của một người đi bộ, em hãy vẽ đồ thị quãng đường – thời gian của người này
Bảng ghi số liệu quãng đường s và thời gian t của người đi bộ
|
Phương pháp giải:
Sử dụng bảng số liệu để vẽ hình
Bước 1: Vẽ hai trục vuông góc cắt nhau tại điểm gốc O, gọi là hai trục tọa độ
+ Trục nằm ngang Ot biểu diễn thời gian theo một tỉ lệ thích hợp
+ Trục thẳng đứng Os biểu diễn độ dài quãng đường theo một tỉ lệ thích hợp
Bước 2: Xác định các điểm có giá trị s và t tương ứng
Bước 3: Nối các điểm đã vẽ ở bước 2 lại với nhau ta có đồ thị quãng đường – thời gian.
Lời giải chi tiết:
Lời giải chi tiết:
Câu hỏi tr 56 VD
| Trong trường hợp nào thì đồ thị quãng đường – thời gian có dạng là một đường thẳng nằm ngang? |
Lời giải chi tiết:
Trường hợp đồ thị quãng đường – thời gian là một đường thẳng nằm ngang khi quãng đường không thay đổi mà thời gian thay đổi => Vật ở trạng thái dừng lại.
Câu hỏi tr 57 Câu 6
|
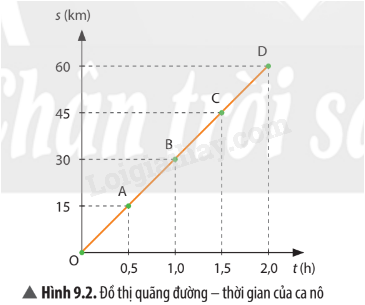
Từ đồ thị ở Hình 9.3, hãy nêu cách tìm:
a) Thời gian để ca nô đi hết quãng đường 60 km. b) Tốc độ của ca nô |
Phương pháp giải:
Quan sát, phân tích dữ liệu
Biểu thức tính tốc độ của vật: \(v = \frac{s}{t}\)
Lời giải chi tiết:
a) Ta có tốc độ của vật trong quá trình chuyển động không đổi nên thời gian để ca bô đi hết quãng đường 60 km là:
\(\begin{array}{l}\frac{{{s_1}}}{{{t_1}}} = \frac{{{s_2}}}{{{t_2}}} \Leftrightarrow \frac{{30}}{1} = \frac{{60}}{{{t_2}}}\\ \Rightarrow {t_2} = 2(h)\end{array}\)
b) Tốc độ của ca nô là:
\(v = \frac{{{s_1}}}{{{t_1}}} = \frac{{30}}{1} = 30(km/h)\)
Câu hỏi tr 57 VD
| Cách mô tả một chuyển động bằng đồ thị quãng đường – thời gian có ưu điểm gì? |
Lời giải chi tiết:
Từ đồ thị quãng đường – thời gian cho trước, ta có thể tìm được quãng đường vật đi hoặc tốc độ hay thời gian chuyển động của vật.
Câu hỏi tr 58 BT 1
|
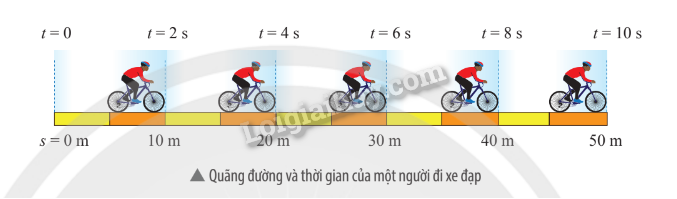
1: Dựa vào các thông tin về quãng đường và thời gian của một người đi xe đạp trong hình dưới, hãy: a) Lập bảng ghi các giá trị quãng đường s và thời gian t tương ứng của người này. b) Vẽ đồ thị quãng đường – thời gian của người đi xe đạp nói trên.
|
Phương pháp giải:
Quan sát hình
Lời giải chi tiết:
a)
|
t (s) |
0 |
2 |
4 |
6 |
8 |
10 |
|
s (m) |
0 |
10 |
20 |
30 |
40 |
50 |
b)
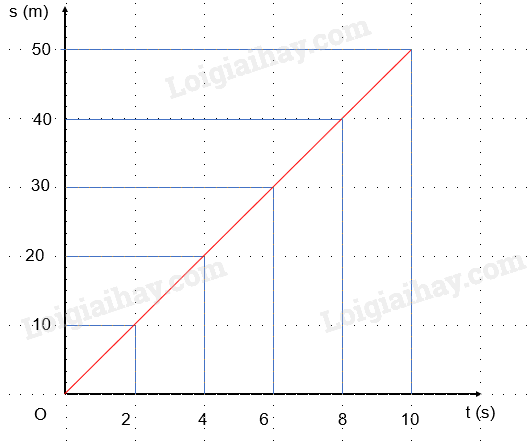
Câu hỏi tr 58 BT 2
|
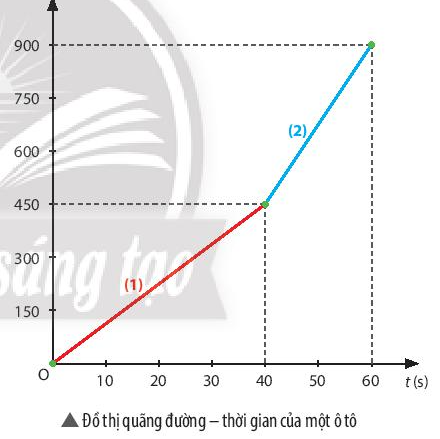
2. Dựa vào đồ thị quãng đường – thời gian của ô tô (hình bên) để trả lời các câu hỏi sau:
a) Sau 50 giây, xe đi được bao nhiêu mét? b) Trên đoạn đường nào xe chuyển động nhanh hơn? Xác định tốc độ của xe trên mỗi đoạn đường. |
Phương pháp giải:
Quan sát hình vẽ
Biểu thức tính tốc độ của vật \(v = \frac{s}{t}\)
Lời giải chi tiết:
a)Từ đồ thị ta thấy t = 50 s, thì xe đi được quãng đường là s = 675 m
b) Tốc độ trung bình trên đoạn đường (1) là: \({v_{tb1}} = \frac{{\Delta {s_1}}}{{\Delta {t_1}}} = \frac{{150}}{{10}} = 15(m/s)\)
Tốc độ trung bình trên đoạn đường (2) là: \({v_{tb2}} = \frac{{\Delta {s_2}}}{{\Delta {t_2}}} = \frac{{900 - 675}}{{10}} = 22,5(m/s)\)
=> Trên đoạn đường (2), xe chuyển động nhanh hơn