Giải Bài 8 trang 106 sách bài tập toán 7 tập 1 - Cánh diều

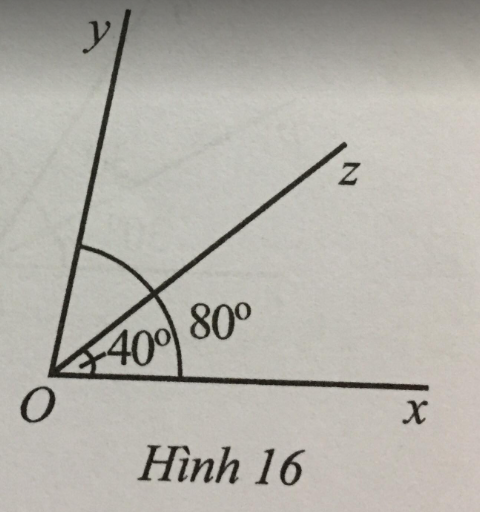
Ở Hình 16 có

Đề bài

Ở Hình 16 có \(\widehat {xOz} = 40^\circ ,\widehat {xOy} = 80^\circ \). Tia Oz có là tia phân giác của góc xOy hay không?

Phương pháp giải - Xem chi tiết

Tia Oz là tia phân giác của góc xOy khi \(\widehat{xOz}=\widehat{yOz}=\dfrac{1}{2}.\widehat{xOy}\)

Lời giải chi tiết

Ta có: \(\widehat {zOy} = \widehat {xOy} - \widehat {xOz} = 80^\circ - 40^\circ = 40^\circ \)

Ta được: \(\widehat {zOy}= \widehat {xOz}=\dfrac{1}{2}.\widehat{xOy}\).

Vậy tia Oz là tia phân giác của góc xOy.