Giải bài 8 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo

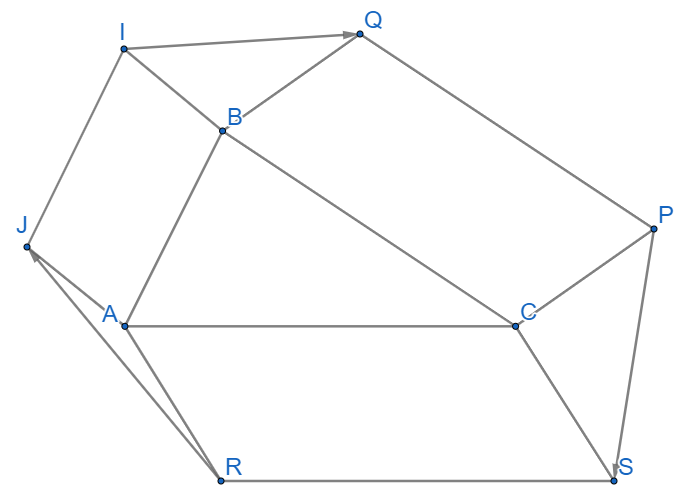
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS

Đề bài

Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \).

Phương pháp giải - Xem chi tiết

Bước 1: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \)

Bước 2: Xác định các cặp vectơ đối nhau từ các hình bình hành \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau với ABCD là hình bình hành

Bước 3: Sử dụng tính chất của vectơ đối \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau thì\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 \)

Lời giải chi tiết

\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)

\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)

Danh Mục

Giải bài 8 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo

Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS