Bài 54 trang 47 SBT toán 7 tập 2

Giải bài 54 trang 47 sách bài tập toán 7. Cho ba tam giác cân ABC, DBC, EBC chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.

Đề bài

Cho ba tam giác cân \(ABC, DBC, EBC\) chung đáy \(BC.\) Chứng minh rằng ba điểm \(A, D, E\) thẳng hàng.

Phương pháp giải - Xem chi tiết

Ta sử dụng:

+) Tính chất tam giác cân

+) Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó

Lời giải chi tiết

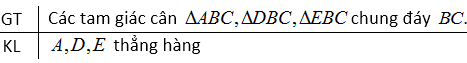
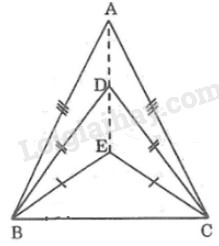
Vì \(∆ABC\) cân tại \(A ,\) suy ra \(AB = AC\)

Nên \(A\) thuộc đường trung trực của \(BC\) (1) (Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó)

Vì \(∆DBC\) cân tại \(D,\) suy ra \(DB = DC\)

Nên \(D\) thuộc đường trung trực của \(BC\) (2) (Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó)

Vì \(∆EBC\) cân tại \(E,\) suy ra \(EB = EC\)

Nên \(E\) thuộc đường trung trực của \(BC\) (3) (Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó)

Từ (1), (2) và (3) \(\Rightarrow A, D, E\) thẳng hàng.