Bài 3.4 trang 130 SBT hình học 11

Đề bài

Cho hình lăng trụ tam giác \(ABC.A’B’C’\) có độ dài cạnh bên bằng \(a\). Trên các cạnh bên \(AA’,BB’,CC’\) ta lấy tương ứng các điểm \(M, N, P\) sao cho \(AM + BN + CP = a\)

Chứng minh rằng mặt phẳng \((MNP)\) luôn luôn đi qua một điểm cố định.

Quảng cáo

Lời giải chi tiết

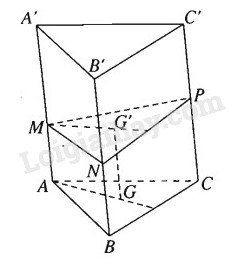
Gọi G và  G’ lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:

\(\displaystyle \eqalign{
& \,\,\,\,\overrightarrow {GG'} = \overrightarrow {GA} + \overrightarrow {AM} + \overrightarrow {MG'} \cr 
& + \,\,\overrightarrow {GG'} = \overrightarrow {GB} + \overrightarrow {BN} + \overrightarrow {NG'} \cr 
& \,\,\,\,\,\overrightarrow {GG'} = \overrightarrow {GC} + \overrightarrow {CP} + \overrightarrow {PG'} \cr} \)

Cộng từng vế với vế ta có:

\(\displaystyle 3\overrightarrow {GG'}  = \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right) \) \(\displaystyle + \left( {\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} } \right) \) \(\displaystyle + \left( {\overrightarrow {MG'}  + \overrightarrow {NG'}  + \overrightarrow {PG'} } \right)\)

Vì G là trọng tâm của tam giác ABC nên \(\displaystyle \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \) và G’ là trọng tâm của tam giác MNP nên \(\displaystyle \overrightarrow {MG'}  + \overrightarrow {NG'}  + \overrightarrow {PG'}  = \overrightarrow 0 \).

Do đó: \(\displaystyle 3\overrightarrow {GG'}  = \overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} \)

Hay \(\displaystyle \overrightarrow {GG'}  = {1 \over 3}\left( {\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} } \right) \) \(\displaystyle = {1 \over 3}\overrightarrow {AA'} \)

Vì điểm G cố định và \(\displaystyle {1 \over 3}\overrightarrow {AA'} \) là vectơ không đổi nên G’ là điểm cố định. Vậy mặt phẳng  (MNP) luôn luôn đi qua điểm G’ cố định.

 Loigiaihay.com