Giải bài 3 trang 99 SGK Toán 7 tập 2 - Cánh diều

Cho tam giác nhọn ABC. a) Vẽ H là hình chiếu của B trên đường thẳng AC; b) Vẽ K là hình chiếu của H trên đường thẳng AB; c) Chứng minh rằng: HK < BH < BC.

Đề bài

Cho tam giác nhọn ABC.

a) Vẽ H là hình chiếu của B trên đường thẳng AC;

b) Vẽ K là hình chiếu của H trên đường thẳng AB;

c) Chứng minh rằng: HK < BH < BC.

Phương pháp giải - Xem chi tiết

a) H là hình chiếu của B trên đường thẳng AC tức \(BH \bot AC;H \in AC\).

b) K là hình chiếu của H trên đường thẳng AB tức \(KH \bot AB;K \in AB\).

c) Dựa vào tính chất của đường vuông góc và đường xiên.

Lời giải chi tiết

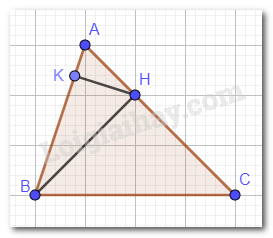
a) Từ B kẻ đường thẳng vuông góc với AC, cắt AC tại H.

Ta được điểm H là hình chiếu của B trên đường thẳng AC.

b) Từ H kẻ đường thẳng vuông góc với AB, cắt AB tại K.

Ta được điểm K là hình chiếu của H trên đường thẳng AB.

c) Trong tam giác ABC có: \(BH \bot AC\) nên BH < BC (BH là đường vuông góc, BC là đường xiên).

Trong tam giác AHB có: \(KH \bot AB\) nên HK < HB (HK là đường vuông góc, HB là đường xiên).

Vậy HK < BH < BC.