Giải Bài 21 trang 111 sách bài tập toán 7 tập 1 - Cánh diều
Tìm số đo góc BCD trong Hình 33.
Đề bài
Tìm số đo góc BCD trong Hình 33.
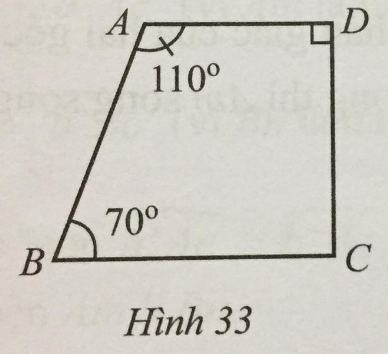
Phương pháp giải - Xem chi tiết
Để tính số đo của góc BCD, ta cần chứng minh AD song song với BC.
Lời giải chi tiết
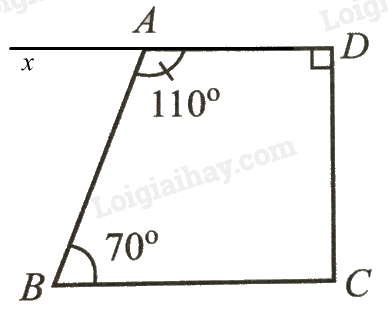
Vẽ Ax là tia đối của AD.
Vì \(\widehat {xAB}\) và \(\widehat {BAD}\) là hai góc kề bù nên \(\widehat {xAB} + \widehat {BAD} = 180^\circ\)
hay \(\widehat {xAB} + 110^\circ = 180^\circ\) suy ra \(\widehat {xAB} = 180^\circ - 110^\circ = 70^\circ\)
Do đó \(\widehat {xAB} = \widehat B = 70^\circ\)
Mà hai góc này ở vị trí so le trong nên AD // BC.
Suy ra \(\widehat D + \widehat C = 180^\circ \) (hai góc trong cùng phía) nên \(\widehat {BCD} = 180^\circ - \widehat D = 180^\circ - 90^\circ = 90^\circ \).


