Giải bài 11 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2

Cho hai tiếp tuyến MA và MB của đường tròn (O). Gọi N là điểm sao cho MANB là một hình bình hành. a) Giả sử N không nằm trên (O), NA và NB cắt (O) lần lượt tại D và C. - Chứng minh rằng ABC là tam giác cân tại đỉnh A. - Chứng minh rằng hai cung BC và AD có số đo bằng nhau. b) Giả sử N nằm trên (O). - Chứng minh rằng MAB là tam giác đều. - Tính độ dài cung AB và diện tích của hình quạt tròn ứng với cung AB, biết rằng đường tròn (O) có bán kính bằng 6cm.

Đề bài

Cho hai tiếp tuyến MA và MB của đường tròn (O). Gọi N là điểm sao cho MANB là một hình bình hành.

a) Giả sử N không nằm trên (O), NA và NB cắt (O) lần lượt tại D và C.

- Chứng minh rằng ABC là tam giác cân tại đỉnh A.

- Chứng minh rằng hai cung BC và AD có số đo bằng nhau.

b) Giả sử N nằm trên (O).

- Chứng minh rằng MAB là tam giác đều.

- Tính độ dài cung AB và diện tích của hình quạt tròn ứng với cung AB, biết rằng đường tròn (O) có bán kính bằng 6cm.

Phương pháp giải - Xem chi tiết

a) + Gọi E là giao điểm của AO và BC. Chứng minh $OE \bot BC$.

+ Chứng minh tam giác BOC cân tại O, suy ra OE là đường cao đồng thời là đường trung trực của BC. Từ đó chứng minh được $AB = AC$ nên tam giác ABC cân tại A.

+ Chứng minh tương tự, tam giác ADB cân tại B.

+ Chứng minh $\widehat {BAC} = \widehat {{B_1}}$, từ đó chứng minh được sđ$\overset\frown{BC}$=sđ$\overset\frown{AD}$.

b) + Gọi E là giao điểm của AO và BN.

+ Chứng minh hình bình hành AMBN là hình thoi, suy ra $AN = BN$ (1).

+ Chứng minh $OE \bot BN$, chứng minh tam giác OBN cân tại O nên OE là đường cao đồng thời là đường trung trực của BN, từ đó chứng minh được$AB = AN$ (2).

+ Từ (1) và (2) chứng minh được tam giác ABN đều. Do đó, tam giác MAB đều.

+ Chứng minh được sđ$\overset\frown{AB}$_nhỏ $ = 2\widehat {ANB} = {120^o}$ từ đó tính được độ dài cung AB và diện tích của hình quạt tròn ứng với cung AB.

Lời giải chi tiết

a) Gọi E là giao điểm của AO và BC.

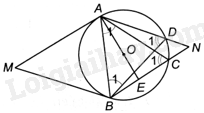
Vì MA là tiếp tuyến của (O) nên $MA \bot AE$, BC//MA (do MANB là hình bình hành) nên $AE \bot BC$ hay $OE \bot BC$.

Tam giác OBC có: $OB = OC$ nên tam giác BOC cân tại O, do đó OE là đường cao đồng thời là đường trung trực của BC. Mà A thuộc đường thẳng OE nên $AB = AC$. Do đó, ABC là tam giác cân tại A.

Chứng minh tương tự ta có tam giác ADB cân tại B.

Ta có: $\widehat {{D_1}} = \widehat {{C_1}}$ (góc nội tiếp đường tròn (O) cùng chắn cung nhỏ AB). Tức là hai tam giác cân ABC và BAD có các góc ở đáy bằng nhau. Do đó, hai góc ở đỉnh cũng bằng nhau. Suy ra $\widehat {BAC} = \widehat {{B_1}}$.

Mà BAC là góc nội tiếp, BOC là góc ở tâm cùng chắn cung BC nên ta có sđ$\overset\frown{BC}=\widehat{BOC}=2\widehat{BAC}$.

Tương tự ta có: sđ$\overset\frown{AD}=\widehat{AOD}=2\widehat{{{B}_{1}}}$.

Do đó, sđ$\overset\frown{BC}$=sđ$\overset\frown{AD}$.

b) Gọi E là giao điểm của AO và BN.

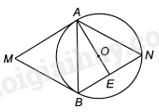
Vì MA, MB là hai tiếp tuyến cắt nhau của (O) nên $MA = MB$. Do đó, hình bình hành AMBN là hình thoi, suy ra $AN = BN$ (1).

Vì MA//BN và $AO \bot AM$ (do MA là tiếp tuyến của (O)) nên $AO \bot BN$ hay $OE \bot BN$.

Tam giác OBN có: $OB = ON$ nên tam giác OBN cân tại O. Do đó, OE là đường cao đồng thời là đường trung trực của BN. Vì A thuộc đường thẳng OE nên $AB = AN$ (2).

Từ (1) và (2) ta có: $AN = BN = AB$ nên NAB là tam giác đều. Do đó, tam giác MAB đều.

Suy ra $\widehat {ANB} = {60^o}$. Vì góc nội tiếp ANB chắn cung nhỏ AB của (O) nên sđ$\overset\frown{AB}$_nhỏ $ = 2\widehat {ANB} = {120^o}$.

Độ dài cung nhỏ AB là: ${l_{AB}} = \frac{{120.6.\pi }}{{180}} = 4\pi \left( {cm} \right)$.

Diện tích hình quạt tròn ứng với cung AB là: ${S_{AB}} = \frac{{120}}{{360}}{.6^2}.\pi = 12\pi \left( {c{m^2}} \right)$.

Danh Mục

Giải bài 11 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2