Giải bài 1 trang 69 SGK Toán 8 – Cánh diều
Cho tam giác ABC có ba đường phân giácAD, BE, CF. Biết
Đề bài
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết \(AB = 4,\,\,BC = 5,\,\,CA = 6\). Tính BD, CE, AF.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính chất đường phân giác để tính độ dài các cạnh.
Lời giải chi tiết
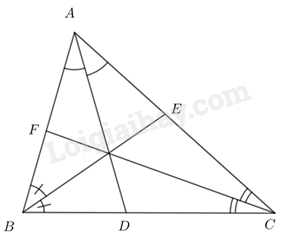
Có AD là đường phân giác trong tam giác ABC nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{{DB}}{{DC}} = \frac{4}{6} = \frac{2}{3} \) nên \(DC = \frac{3}{2}DB\)
Mà \(DB + DC = BC \) hay \(DB + \frac{3}{2}DB = 5 \) nên \(DB = 2\)
Có BE là đường phân giác trong tam giác ABC nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{CB}} = \frac{4}{5} \) suy ra \(AE = \frac{4}{5}CE\)
Mà \(AE + EC = AC \) hay \(\frac{4}{5}CE + CE = 6 \) nên \(CE = \frac{{10}}{3}\)
Có CF là đường phân giác trong tam giác ABC nên \(\frac{{AF}}{{FB}} = \frac{{CA}}{{CB}} = \frac{6}{5} \) suy ra \(FB = \frac{6}{5}AF\)
Mà \(AF + FB = AB \) hay \(AF + \frac{5}{6}AF = 4 \) nên \(AF = \frac{{24}}{{11}}\).


