Bài 69 trang 49 SBT Hình học 10 Nâng cao

Đề bài

Cho tứ giác \(ABCD\) có \(AB = a ,  \widehat {CAB} = \alpha  ,\)\(  \widehat {DBA} = \beta  ,  \widehat {DAC} = \alpha ' ,  \widehat {CBD} = \beta '\). Tính độ dài cạnh \(CD\).

Lời giải chi tiết

(h.62).

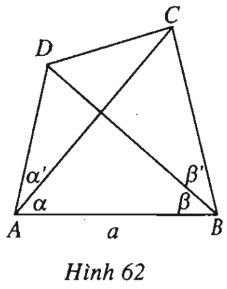
Tính \(AD\) và \(AC\) như bài 68 ta được

\(AD = \dfrac{{a\sin \beta }}{{\sin (\alpha  + \alpha ' + \beta )}} , \)

\( AC = \dfrac{{a\sin (\beta  + \beta ')}}{{\sin (\alpha  + \beta  + \beta ')}}\).

Sau đó áp dụng đính lí cosin vào tam giác \(ACD\) ta có

\(C{D^2} = A{C^2} + A{D^2} - 2AC.AD.\cos \alpha '\).

Loigiaihay.com