Bài 4.41 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức

Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau: a) (SAD) và (SBC) b) (SAB) và (SCD) c) (SAC) và (SBD)

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:

a) (SAD) và (SBC)

b) (SAB) và (SCD)

c) (SAC) và (SBD)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Tìm hai điểm chung A và B của \(\alpha \) và \(\beta \).

- Đường thẳng AB là giao tuyến cần tìm.

Quảng cáo

Lời giải chi tiết

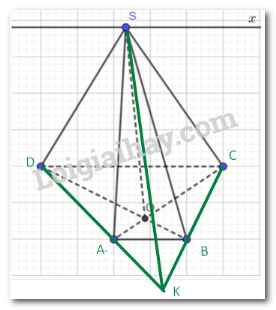
a) Gọi giao điểm của AD và BC là K.

Ta có: SK cùng thuộc (SAD) và (SBC).

Vậy SK là giao tuyến của (SAD) và (SBC).

b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua S và song song với AB và CD.

c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBD).

Suy ra SO là giao tuyến của (SAC) và (SBD).