Bài 3 trang 168 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A, biết \(\widehat A = {50^0}\)  (h.17).

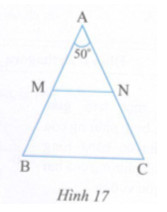
a) Tính \(\widehat B,\widehat C.\)

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng  cân.

c) Chứng minh rằng MN // BC.

Lời giải chi tiết

a)Tam giác ABC có: \(\widehat A + \widehat B + \widehat C = {180^0}.\)   Mà \(\widehat B = \widehat C(\Delta ABC\)  cân tại A) nên \({50^0} + \widehat B + \widehat B = {180^0}\)

\(\Rightarrow {50^0} + 2\widehat B = {180^0} \Rightarrow 2\widehat B = {180^0} - {50^0} = {130^0} \Rightarrow \widehat B = {{{{130}^0}} \over 2} = {65^0}.\)

Ta có: \(\widehat C = \widehat B = {65^0}\)

b) Ta có: \(AM = {{AB} \over 2}\)   (M là trung điểm của AB)

\(AN = {{AC} \over 2}\)   (N là trung điểm của AC)

AB = AC (tam giác ABC cân tại A)

Suy ra Am = AN. Do đó: tam giác AMN cân tại A.

c) Tam giác AMN có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)   mà \(\widehat {AMN} = \widehat {ANM}(\Delta AMN\) cân tại A)

Nên \(\widehat A + 2\widehat {AMN} = {180^0} \Rightarrow \widehat {AMN} = {{{{180}^0} - {{50}^0}} \over 2} = {65^0}.\)

Mà \(\widehat B = {65^0}\)   (chứng minh câu a) nên \(\widehat {AMN} = \widehat B( = {65^0}).\)

Góc AMN và B là hai góc đồng vị. Do đó MN // BC.

Loigiaihay.com