Bài 11 trang 40 SBT Hình học 10 Nâng cao
Giải bài tập Bài 11 trang 40 SBT Hình học 10 Nâng cao
Đề bài
Tam giác \(MNP\) có \(MN=4, MP=8,\) \(\widehat M = {60^0}\).Lấy điểm \(E\) trên tia \(MP\) và đặt \(\overrightarrow {ME} = k\overrightarrow {MP} \). Tìm \(k\) để \(NE\) vuông góc với trung tuyến \(MF\) của tam giác \(MNP.\)
Lời giải chi tiết
(h.28).
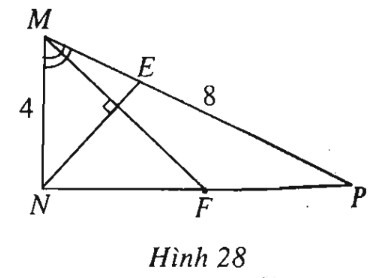
\(\begin{array}{l}\overrightarrow {NE} = \overrightarrow {NM} + \overrightarrow {ME} = k\overrightarrow {MP} - \overrightarrow {MN},\\\overrightarrow {MF} = \dfrac{1}{2}(\overrightarrow {MP} + \overrightarrow {MN} ).\\NE \bot MF\\ \Leftrightarrow(\overrightarrow {MP} + \overrightarrow {MN} ).(k\overrightarrow {MP} - \overrightarrow {MN} ) = 0\\\Leftrightarrow \,k = \dfrac{{\overrightarrow {MN} .(\overrightarrow {MP} + \overrightarrow {MN} )}}{{\overrightarrow {MP} .(\overrightarrow {MP} + \overrightarrow {MN} )}}\\ = \dfrac{{\overrightarrow {MN} .\overrightarrow {MP} + {{\overrightarrow {MN} }^2}}}{{{{\overrightarrow {MP} }^2} + \overrightarrow {MN} .\overrightarrow {MP} }}\\ = \dfrac{{16 + 16}}{{64 + 16}} = \dfrac{2}{5}.\end{array}\)
Loigiaihay.com

